Code Structure

Full details on the class hierarchy and internal structure of the code can be found in the Doxygen documentation for SU2. A brief description for the major C++ classes is given on this page.

Note: The images below can be out of sync with the current version of the code.

The objective of this section is to introduce the C++ class structure of SU2 at a high level. The class descriptions below focus on the structure within SU2_CFD (the main component of SU2), but many of the classes are also used in the other modules. Maximizing the flexibility of the code was a fundamental driver for the design of the class architecture, and an overview of the collaboration diagram of all classes within SU2_CFD is shown below.

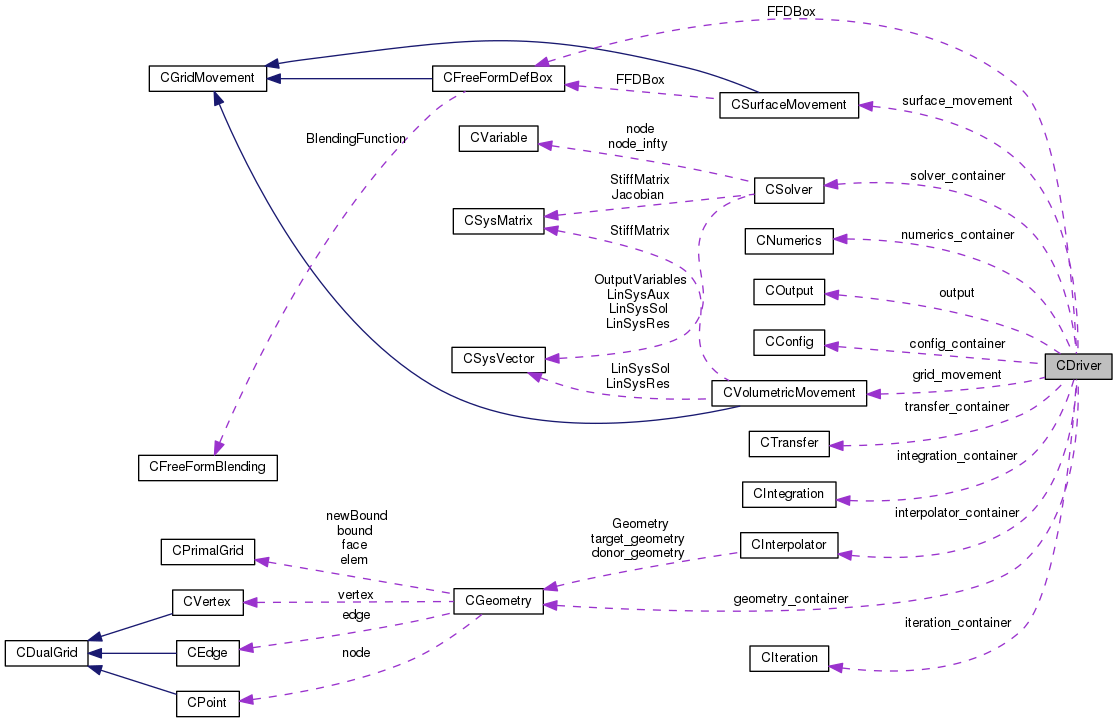
At the highest level, SU2_CFD has a driver class, CDriver, that controls the solution of a multiphysics simulation. The CDriver class is responsible for instantiating all of the geometry, physics packages, and numerical methods needed to solve a particular problem. The CDriver class within SU2_CFD instantiates many classes, including the following:

• CConfig - Reads and stores the problem configuration, including all options and settings from the input file (extension .cfg).
• COutput - Writes the output of the simulation in a user-specified format (Paraview, Tecplot, CGNS, comma-separated values, etc.).
• CIntegration - Solves the particular governing equations by calling the child classes CMultiGridIntegration, CSingleGridIntegration. This is used for both multigrid or single-grid calculations, and it connects the subclasses CGeometry, CSolver, and CNumerics for performing integration in time and space.
• CIteration - Classes that complete an iteration of a single physics package, e.g., fluid or structure.

The core capabilities of the computational tool are embedded within the CGeometry, CSolver, and CNumerics classes that manage the geometry, the main solver functionality (definition of the terms in the PDE), and the numerical methods, respectively. In the next subsection, these three classes will be discussed.

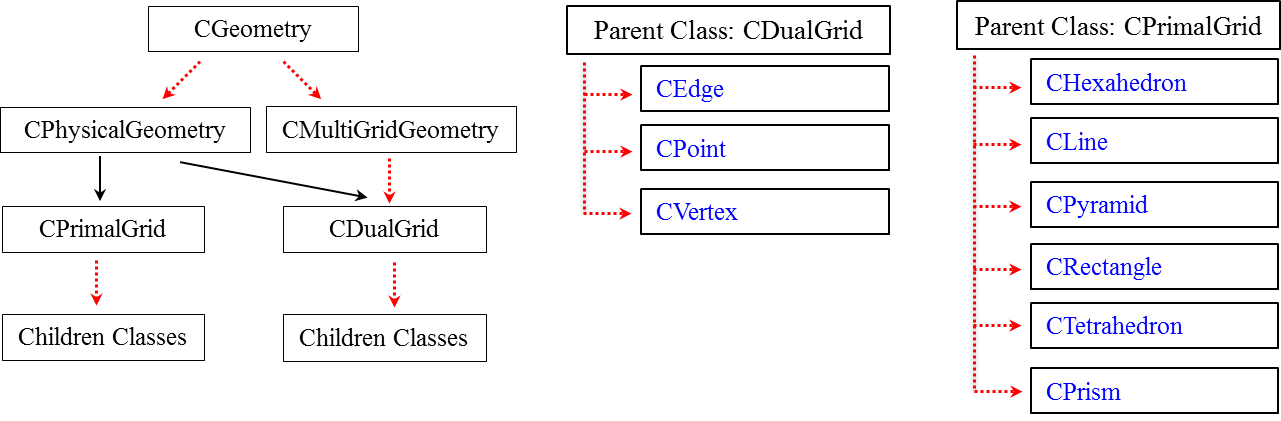
CGeometry Class

This class reads and processes the input mesh file (extension .su2), and it includes several child classes, such as: CPhysicalGeometry - Constructs the dual mesh structure from the primal mesh. Note that the FVM formulation in SU2 is based on the dual mesh with edge-based data structures.

• CMultiGridGeometry - If multigrid is requested, this class automatically creates consecutively coarser meshes from the original input mesh using a control volume agglomeration procedure. These coarse grid levels are then used for multigrid calculations.
• CPrimalGrid and CDualGrid - Two classes (see Fig. below) that are used for defining the geometrical characteristics of the primal and dual grids.

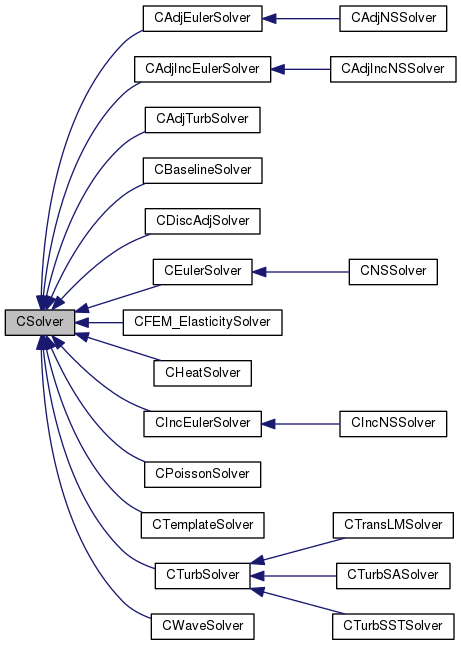
CSolver Class

In this class, the solution procedure is defined. Each child class of CSolver represents a solver for a particular set of governing equations. These solver classes contain subroutines with instructions for computing each spatial term of the PDE, e.g., loops over the mesh edges to compute convective and viscous fluxes, loops over the mesh nodes to compute source terms, and routines for imposing various boundary condition types for the PDE.

One or more of these child classes will be instantiated depending on the desired physics, and several examples are:

• CEulerSolver - For the Euler equations (compressible or incompressible).
• CTurbSolver - For a turbulence model.
• CAdjEulerSolver - For the adjoint equations of the Euler equations.

The solver containers also lead to one of the defining features of SU2: the ability to easily construct multi-physics problems by combining multiple solvers representing different physics. For example, the mean flow equations are easily coupled to the S-A turbulence model by instantiating both the CNSSolver class and the CTurbSASolver class. These two solver containers will control the solution of the different PDEs while being integrated simultaneously, and the information they contain can be freely passed back and forth. Another example of this flexibility arises when solving the adjoint equations. For instance, when solving the adjoint Euler equations, both the CAdjEulerSolver and the CEulerSolver classes are instantiated, as the adjoint equations require a copy of the flow solution that will be read from a solution file and stored by the CEulerSolver class.

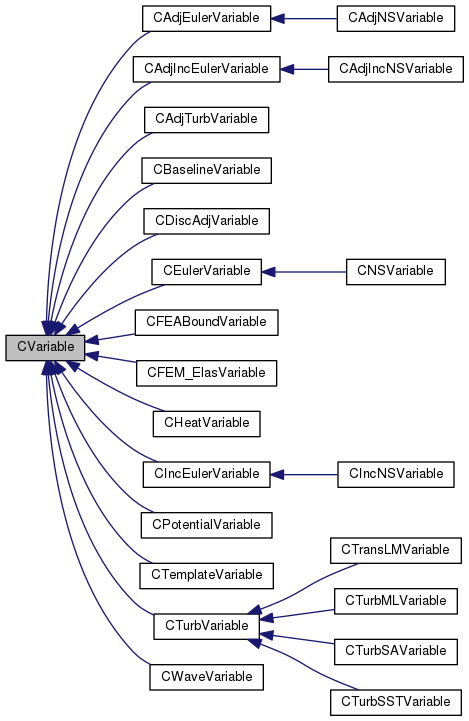
The solver classes call the CVariable class for storing unknowns and other variables pertinent to the PDE at each mesh node, several classes in CNumerics in order to specify a spatial discretization of the governing equations (to be discussed below), and, if necessary, container classes for holding the matrices and vectors needed by linear solvers. A detailed list of all child classes found within CSolver is given in the Fig. below, but in general, these classes can be briefly described as follows:

• CVariable - Used to store variables at every point in the grid, such as the conservative variables (unknowns of the PDE). Depending on the system of equations being solved, CVariable instantiates a certain child class and stores a set of variables particular to that problem at each grid node. For example, the CNSVariable child class stores the variables for the Navier-Stokes equations, which will include viscosity, while the CEulerVariable child class does not need to store viscosity. A detailed list of all these child classes is given in the Fig. below.
• CSysMatrix - Stores values for the Jacobians of fluxes and source terms in a sparse matrix structure for implicit calculations. It includes various methods for solving a linear system, including Krylov methods such as GMRES and BiCGSTAB, in addition to several preconditioning techniques, such as Jacobi, LU-SGS, or line implicit preconditioning.
• CSysVector - Holds and manipulates vectors needed by the linear solvers in combination with CSysMatrix to store the sparse matrix representation of the Jacobian.

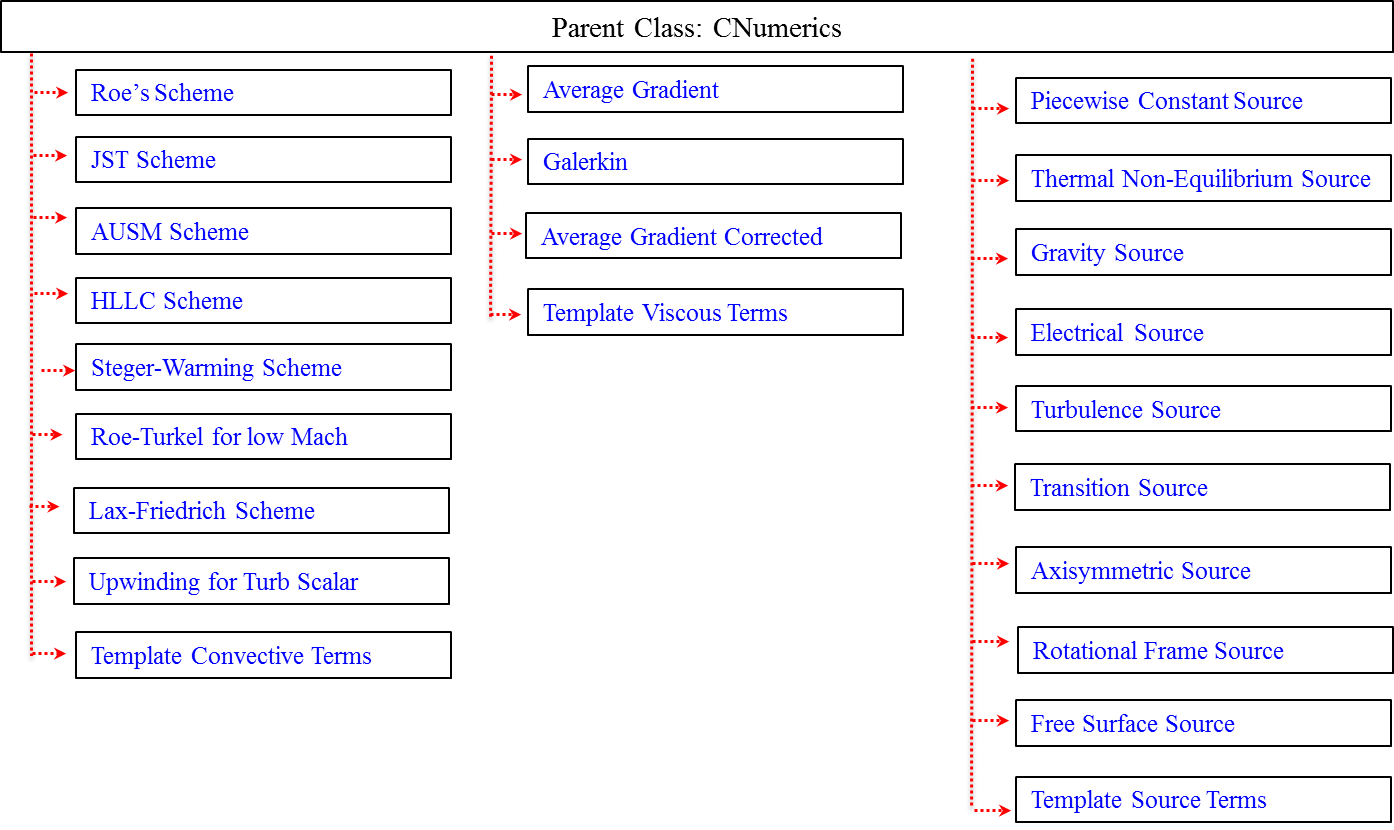
CNumerics Class

This class discretizes each system of governing equations using the numerical schemes specified in the input file. There are several child classes that provide a wide range of discretization techniques for convective fluxes, viscous fluxes, and any source terms that might be present in a given PDE. For example, if one is interested in solving the Navier-Stokes equations expressed in a non-inertial frame, CNumerics would call one child class corresponding to the convective scheme, one corresponding to the viscous terms, and a third for the discretization of the momentum source term that arises from the transformation of the equations to a rotating reference frame.

As another example, during a single iteration of an implicit calculation, methods in the CNumerics classes would compute the flux contributions and Jacobians at each node (using the variables stored in the CVariable class). These flux and Jacobian values are transferred back to the CSolver class, and the CSolver class calls routines within CSysMatrix in order to solve the resulting linear system of equations for the solution update. The Fig. below shows a list of the various capabilities in the CNumerics class.