Quick Start

Welcome to the Quick Start Tutorial for the SU2 software suite. This tutorial is intended to demonstrate some of the key features of the analysis and design tools in an easily accessible format. Completion of this tutorial only requires a few minutes. If you haven’t done so already, please visit the Download and Installation pages to obtain the most recent stable release of the software and details for installation. This tutorial requires only the SU2_CFD tool from the SU2 suite (and optionally the SU2_CFD_AD tool).

• Goals
• Resources
• Tutorial
  • Background
  • Problem Setup
  • Mesh Description
  • Direct Problem Configuration
  • Running SU2 Direct Analysis
  • Direct Analysis Results
  • Running SU2 Adjoint Analysis
  • Adjoint Analysis Results
• Conclusions

Goals

Upon completing this simple tutorial, the user will be familiar with performing the flow and continuous (and/or discrete) adjoint simulation of external, inviscid flow around a 2D geometry and be able to plot both the flow solution and the surface sensitivities that result. The specific geometry chosen for the tutorial is the NACA 0012 airfoil. Consequently, the following capabilities of SU2 will be showcased in this tutorial:

• Steady, 2D, Euler and Continuous/Discrete Adjoint Euler equations
• Multigrid
• JST numerical scheme for spatial discretization
• Euler implicit time integration
• Euler Wall and Farfield boundary conditions

Resources

The files necessary to run this tutorial are included in the SU2/QuickStart/ of the SU2 repository. Some auxiliary files, useful to automate the tutorial simulations and the visualization of results, may be found in the QuickStart directory of the Tutorials repository. Files for other tutorials may be found in the same repository. For a start, two files are needed as input to the code: a configuration file describing the options for the particular problem, and the corresponding computational mesh file.

Tutorial

The following tutorial will walk you through the steps required to compute the flow and adjoint solutions around the NACA 0012 airfoil using SU2. Again, we assume that you have already obtained and compiled the SU2_CFD code (either individually, or as part of the complete SU2 package) for a serial computation. If you have yet to complete this requirement, please see the Download and Installation pages.

Background

The NACA 0012 airfoil is one of the four-digit wing sections developed by the National Advisory Committee for Aeronautics (NACA), and it is a widely used geometry for many CFD test cases. The numbering system is such that the first number indicates the maximum camber (in percent of chord), the second shows the location of the maximum camber (in tens of percent of chord) and the last two digits indicate the maximum thickness (in percent of chord). More information on these airfoil sections can be found here or in the book ‘Theory of Wing Sections’ by Abbott and von Doenhoff.

Problem Setup

This problem will solve the Euler equations on the NACA 0012 airfoil at an angle of attack of 1.25 degrees, using air with the following freestream conditions:

• Pressure = 101325 Pa
• Temperature = 273.15 K
• Mach number = 0.8

The aim is to find the flow solution and the adjoint solution with respect to an objective function defined as the drag on the airfoil.

Mesh Description

The unstructured mesh provided is in the native .su2 format. It consists of 10216 triangular cells, 5233 points, and two boundaries (or “markers”) named airfoil and farfield. The airfoil surface uses a flow-tangency Euler wall boundary condition, while the farfield uses a standard characteristic-based boundary condition. The figure below gives a view of the mesh.

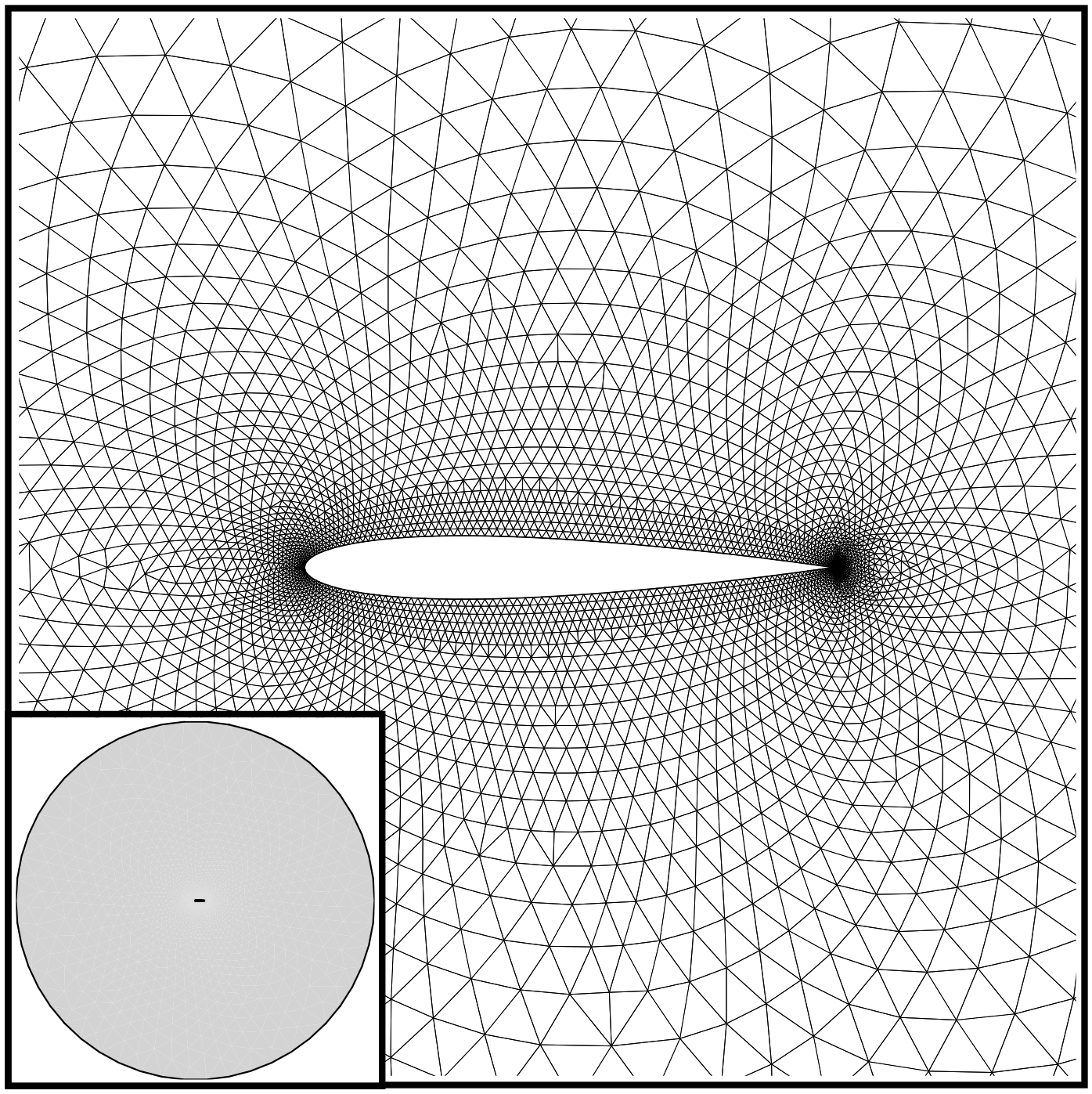
Figure (1): Far-field and zoom view of the computational mesh.

Direct Problem Configuration

Aside from the mesh, the only other file required to run the SU2_CFD solver details the configuration options. It defines the problem, including all options for the numerical methods, flow conditions, multigrid, etc., and also specifies the names of the input mesh and output files. In keeping simplicity for this tutorial, only two configuration options will be discussed. More configuration options will be discussed throughout the remaining tutorials.

Upon opening the inv_NACA0012.cfg file in a text editor, one of the early options is the MATH_PROBLEM:

% Mathematical problem (DIRECT, CONTINUOUS_ADJOINT)
MATH_PROBLEM= DIRECT

SU2 is capable of running the direct and adjoint problems for several sets of equations. The direct analysis solves for the flow around the geometry, and quantities of interest such as the lift and drag coefficient on the body will be computed. Solving the adjoint problem leads to an efficient method for obtaining the change in a single objective function (e.g., the drag coefficient) relative to a large number of design variables (surface deformations). The direct and adjoint solutions often couple to provide the objective analysis and gradient information needed by an optimizer when performing aerodynamic shape design. In this tutorial, we will first perform a DIRECT simulation for the NACA 0012 airfoil.

The user can also set the format for the output files:

% Output file format
OUTPUT_FILES= (RESTART, PARAVIEW, SURFACE_CSV)

SU2 can output solution files in the .vtu (ParaView), .dat (Tecplot ASCII), and .szplt (Tecplot binary) formats which can be opened in the ParaView and Tecplot visualization software packages, respectively. We have set the file type to PARAVIEW in this tutorial: in order to visualize the solution, users are encouraged to download and use the freely available ParaView package. The output format for the data on the airfoil boundary is set to SURFACE_CSV (Comma Separated Values): the resulting text file may be plotted with various graphing tools or with LaTeX packages such as PGFPlots. Please note that, if the OUTPUT_FILES option is not present in the configuration file, its default value is (RESTART, PARAVIEW, SURFACE_PARAVIEW).

Running SU2 Direct Analysis

The first step in this tutorial is to solve the Euler equations:

1. Either navigate to the QuickStart/ directory or create a directory in which to run the tutorial. If you have created a new directory, copy the config file (inv_NACA0012.cfg) and the mesh file (mesh_NACA0012_inv.su2) to this directory.
2. Run the executable by entering SU2_CFD inv_NACA0012.cfg at the command line. If you have not set the appropriate environment variables, you may need to specify the path to your SU2_CFD executable in the command line.
3. SU2 will print residual updates with each iteration of the flow solver, and the simulation will finish after reaching the specified convergence criteria.
4. Files containing the flow results (with “flow” in the file name) will be written upon exiting SU2. The flow solution can be visualized in ParaView (.vtu) or Tecplot (.dat or .szplt). More specifically, these files are:
   • flow.vtu (or flow.szplt) - full volume flow solution.
   • surface_flow.csv (or surface_flow.vtu or surface_flow.szplt) - file containing values along the airfoil surface.
   • restart_flow.dat - restart file in an internal format for restarting this simulation in SU2.
   • history.csv (or history.dat) - file containing the convergence history information.

Direct Analysis Results

The following figures were created in ParaView using the SU2 results. These results are contained in the flow.vtu file.

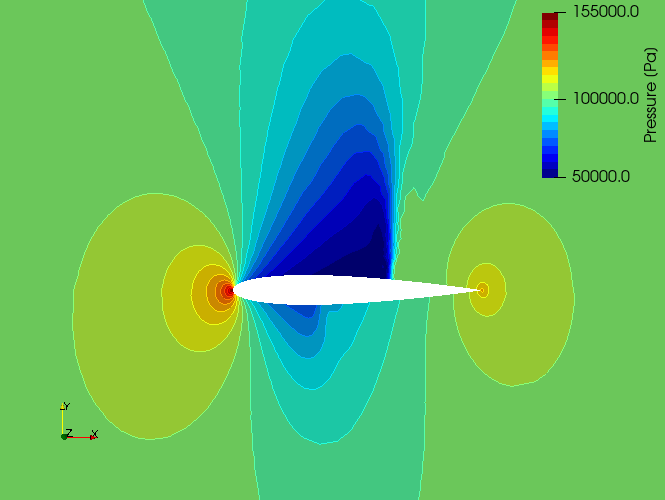
Figure (2): Pressure contours around the NACA 0012 airfoil.

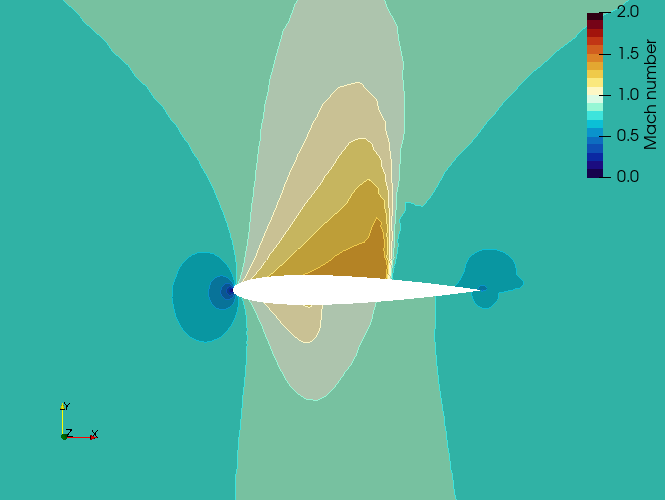
Figure (3): Mach number contours around the NACA 0012 airfoil.

The following plot was created in LaTeX with PGFPlots using the SU2 results. These results are contained in the surface_flow.csv file.

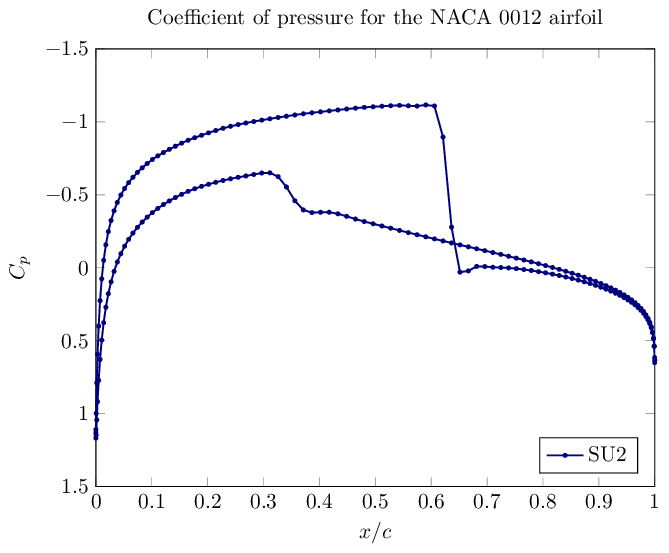
Figure (4): Coefficient of pressure distribution along the airfoil surface. Notice the strong shock on the upper surface (top line) and a weaker shock along the lower surface (bottom line).

Running SU2 Adjoint Analysis

Next, we want to run the adjoint solution to get the sensitivity of the objective function (the drag over the airfoil) to conditions within the flow:

1. Open the config file and change the parameter MATH_PROBLEM from DIRECT to CONTINUOUS_ADJOINT, and the parameter OUTPUT_FILES from (RESTART, PARAVIEW, SURFACE_CSV) to (RESTART, SURFACE_CSV); save this file.
2. Rename (or symlink) the restart file (restart_flow.dat) to “solution_flow.dat” so that the adjoint code has access to the direct flow solution.
3. Run the executable again by entering SU2_CFD inv_NACA0012.cfg at the command line.
4. SU2 will print residual updates with each iteration of the adjoint solver, and the simulation will finish after reaching the specified convergence criteria.
5. Files containing the adjoint results (with “adjoint” in the file name) will be written upon exiting SU2. More specifically, these files are:
   • surface_adjoint.csv (or surface_adjoint.vtu or surface_adjoint.szplt) - file containing adjoint values along the airfoil surface.
   • restart_adj_cd.dat - restart file in an internal format for restarting this simulation in SU2. Note that the name of the objective appears in the file name.
   • history.csv (or history.dat) - file containing the convergence history information.
   • (adjoint.vtu or adjoint.szplt, if requested) - full volume adjoint solution, that can be visualized in ParaView or Tecplot.

Note that as of SU2 v4.1 or later, you can also compute a discrete adjoint for the Euler equations. Assuming that you have built the code with algorithmic differentiation support, you can run the discrete adjoint with the following steps instead:

1. Open the config file and change the parameter MATH_PROBLEM to DISCRETE_ADJOINT, and the parameter OUTPUT_FILES to (RESTART, SURFACE_CSV); save this file.
2. Rename (or symlink) the restart file (restart_flow.dat) to “solution_flow.dat” so that the adjoint code has access to the direct flow solution.
3. Run the executable by entering SU2_CFD_AD inv_NACA0012.cfg at the command line. Note that the SU2_CFD_AD executable will only be available when the source has been compiled with AD support.
4. SU2 will again print residual updates with each iteration of the adjoint solver, and the simulation will finish after reaching the specified convergence criteria.
5. Similar files containing the adjoint results will be written upon exiting SU2.

Adjoint Analysis Results

The following plot was created in LaTeX with PGFPlots using the SU2 results and comparing the output from the continuous and discrete adjoint approaches. These results are contained in the two surface_adjoint.csv files.

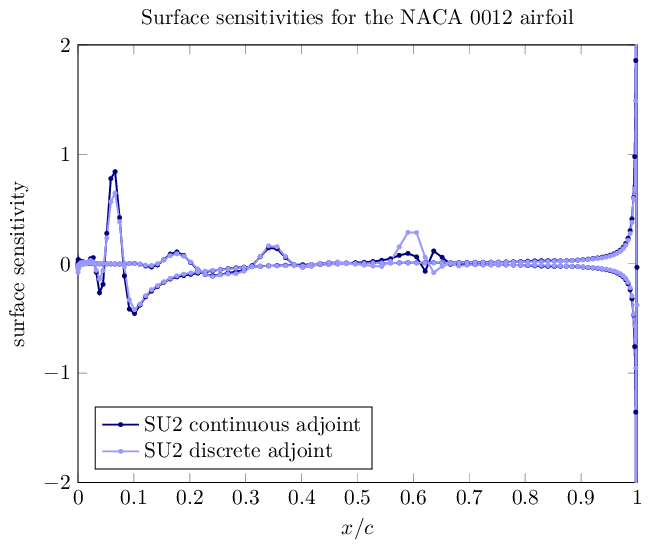
Figure (5): Surface sensitivities. The surface sensitivity is the change in the objective function due to an infinitesimal deformation of the surface in the local normal direction. These values may be refined at each node on the airfoil surface from the flow and adjoint solutions at negligible computational cost using an additional step not described in this tutorial.

Conclusions

Congratulations! You’ve successfully performed your first flow simulations with SU2. Move on to the tutorials to learn much more about using the code, and don’t forget to read through the information in the user’s guide. Having problems with the quick start or visualizing the results? Visit the FAQs page, or see our forum at CFD-online.