Advanced AD Techniques

Algorithmic Differentiation (AD) is a frequently used method to calculate the derivative of a function by means of the transformation of the underlying program which calculates the numerical values of this function. As distinguished from symbolic differentiation an explicit expression for the derivative is never formed. An advantage over FD is that no truncation errors are present, thus the numerical value can be determined up to machine accuracy.

Consider a function y = f(x), using the reverse mode of AD we get

xb = (df/dx)^T yb

with an arbitrary seed vector yb.

Expression Templates

In SU2 we use the AD tool CoDi to enable the computation of arbitrary derivatives. It is based on the Expression Template approach. Here the overloaded operators no longer return the (computationally expensive) result of an expression, but a small temporary object that acts as a placeholder for this particular expression. Using this objects we can build an internal representation of each expression to directly compute and store its partial derivatives during the evaluation of the program. This information is then used to correctly accumulate the gradients (or rather xb) in a second reverse sweep.

The picture below shows the computational graph for the expression φ=cos(v1)v2 and the compile-time representation as object with su2double being the general datatype used throughout SU2.

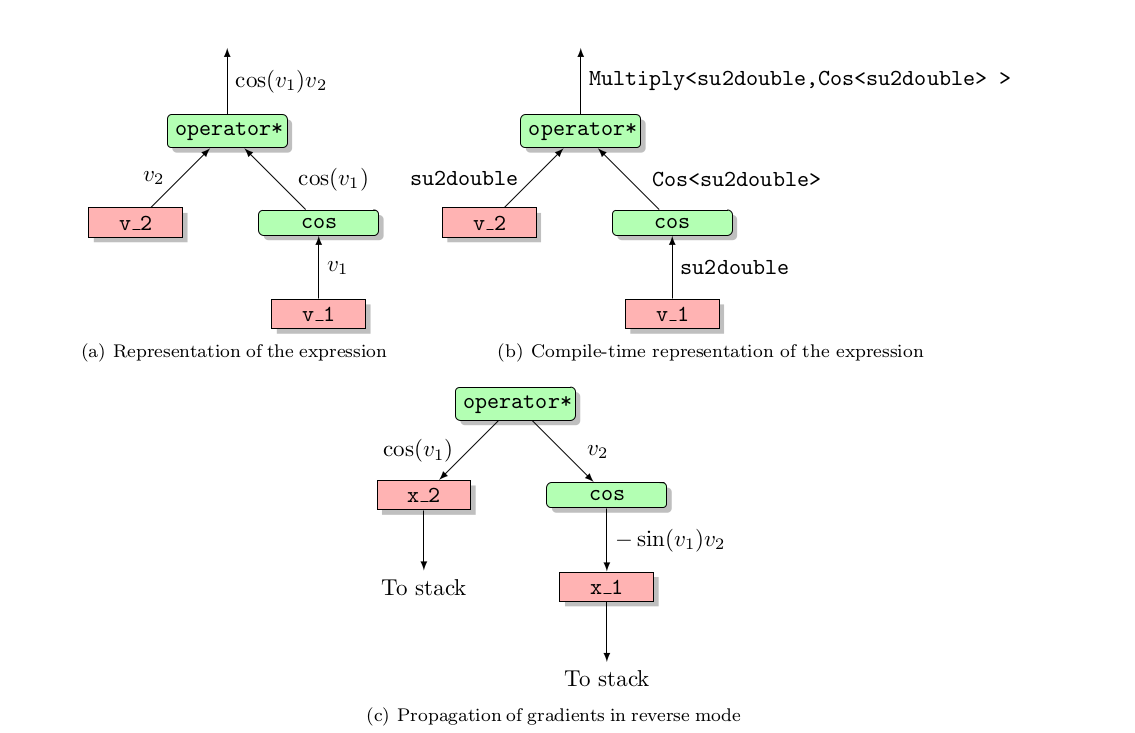
This object can be traversed to compute and store the partial derivatives ∂φ/∂v1=-sin(v1)v2 and ∂φ/∂v2=cos(v1) based on the derivatives of each involved unary or binary operation. If recording is enabled the traversal of the computational graph of each expression is started as soon as it occurs on the right-hand side in a statement. Note that the partial derivatives are only stored if the corresponding argument has some dependency on the input variables set by the user. This kind of dependency or activity tracking is relatively easy to accomplish since every variable stores an index along with its value. A zero index represents passive variables while a non-zero index identifies active variables. This index will be non-zero only if the corresponding variable has been assigned an expression with at least one active variable as an argument.

AD Tool Wrapper

The CoDi library provides a special datatype and is automatically included during the compilation if AD support is requested by the user (see the build instructions for further information). For developers of SU2 there is no need to deal with this library explicitly which is why there are simple wrapper routines for the most important features available. These are for example the following:

• AD::RegisterInput(su2double &var): Registers the variable as input, i.e. sets the index to a non-zero value. The exact value is determined by the AD tool.
• AD::StartRecording(): Starts the recording by enabling the traversal of the computational graphs of each subsequent expression to store the partial derivatives.
• AD::StopRecording(): Stops the recording of information.
• AD::ComputeAdjoint(): Interprets the stored information to compute the gradient.
• AD::Reset(): Deletes all stored information, i.e. the adjoint values and the partial derivatives to enable a new recording.
• AD::ClearAdjoints(): Sets the adjoint values to zero but keeps the derivative information, thereby enabling a new interpretation with a different seed vector yb.

Since the actual interpretation of the adjoints is done by the AD tool, we need some functions to set and extract the derivative information. To account for other datatypes (like for example types that implement the forward mode of AD or types for the complex step method) these functions are enclosed in the namespace SU2_TYPE:

• SU2_TYPE::SetDerivative(su2double &var, double &val): Sets the adjoint value of a variable before calling AD::ComputeAdjoint().
• SU2_TYPE::GetDerivative(su2double &var): Returns the interpreted adjoint value of a variable registered as input. Note: at the moment this function must be called in the same order as AD::RegisterInput(su2double &var).

Local Preaccumulation

To alleviate the high memory requirements we apply the so called local preaccumulation method. Here we compute and store the local Jacobi matrices of certain enclosed code parts instead of storing each individual statement contribution. To illustrate the method consider the code shown in the listing below which computes the volume of 2D elements of the mesh. Without using preaccumulation and if we assume that nDim equals 2 we have to store 12 partial derivative values for the 3 statements (2 ∗ 2 in line 7, 2 ∗ 2 in line 8 and 4 in line 11).

  AD::StartPreacc();
  AD::SetPreaccIn(val_coord_Edge_CG, nDim);
  AD::SetPreaccIn(val_coord_Elem_CG, nDim);
  AD::SetPreaccIn(val_coord_Point, nDim);

  for (iDim = 0; iDim < nDim; iDim++) {
     vec_a[iDim] = val_coord_Elem_CG[iDim]-val_coord_Point[iDim];
     vec_b[iDim] = val_coord_Edge_CG[iDim]-val_coord_Point[iDim];
  }

  Local_Volume = 0.5*fabs(vec_a[0]*vec_b[1]-vec_a[1]*vec_b[0]);
	
  AD::SetPreaccOut(Local_Volume);
  AD::EndPreacc();

  return Local_Volume;

With preaccumulation we only store the derivatives of the variables flagged using AD::SetPreaccIn with respect to the variables flagged with AD::SetPreaccOut. For our example this results in 6 values, which means total saving of memory of 50%. Note that this exemplary code snippet is executed for every element in the mesh. Throughout the code this method is applied at several spots where a clear identification of inputs and outputs was possible.